- E0
[1QC]Per ogni punto \((x,y)\) del piano con \(x,y{\gt}0\) passa un’unica ellissi \(4 x^ 2 + y^ 2 = a\) (con \(a{\gt}0\)). Descrivete la famiglia di curve che in ogni punto sono ortogonali all’ellisse passante per quel punto. Si veda la figura 12.
Soluzione 1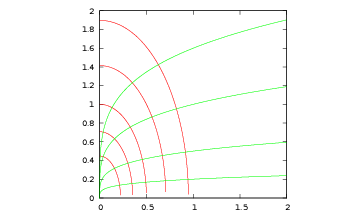
Figure 1 Ellissi (in rosso)e curve a esse ortogonali. [ [1QG]]
EDB — 1QC
View
Italian
Authors:
"Mennucci , Andrea C. G."
.
Managing blob in: Multiple languages