22 Equazioni differenziali[1QB]
Per poter risolvere i seguenti esercizi sarà necessario conoscere alcuni risultati fondamentali, quali: il Teorema di esistenza e unicità locale 1 , il Lemma di Gronwall; e in generale i metodi per analizzare, risolvere e/o studiare qualitativamente le Equazioni Differenziali. Questi si possono per esempio trovare in [ 26 , 21 , 20 , 3 ] .
- E419
[1QC]Per ogni punto \((x,y)\) del piano con \(x,y{\gt}0\) passa un’unica ellissi \(4 x^ 2 + y^ 2 = a\) (con \(a{\gt}0\)). Descrivete la famiglia di curve che in ogni punto sono ortogonali all’ellisse passante per quel punto. Si veda la figura 6.
Soluzione nascosta: [UNACCESSIBLE UUID ’1QF’]
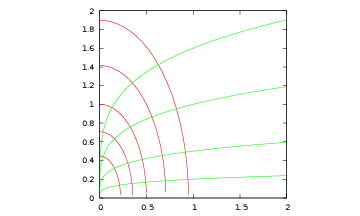
Figura 6 Ellissi (in rosso)e curve a esse ortogonali.
Sia \(I\subseteq {\mathbb {R}}\) intervallo aperto.
Sia \(F:I× ℝ→ (0,∞)\) funzione continua positiva, e sia \(f: I→ℝ\) una funzione differenziabile che risolve l’equazione differenziale
Mostrate allora che \(x\) è sempre crescente, nel qual caso si ha \(f'(x)=\sqrt{F(x,f(x))}\) per ogni \(x\), oppure è sempre decrescente, nel qual caso si ha \(f'(x)=-\sqrt{F(x,f(x))}\); e che dunque \(f\) è di classe \(C^ 1\).
Soluzione nascosta: [UNACCESSIBLE UUID ’1QJ’] [1QK]Prerequisiti:6.
Descrivete tutte le funzioni \(f:ℝ→ℝ\) differenziabili che risolvono
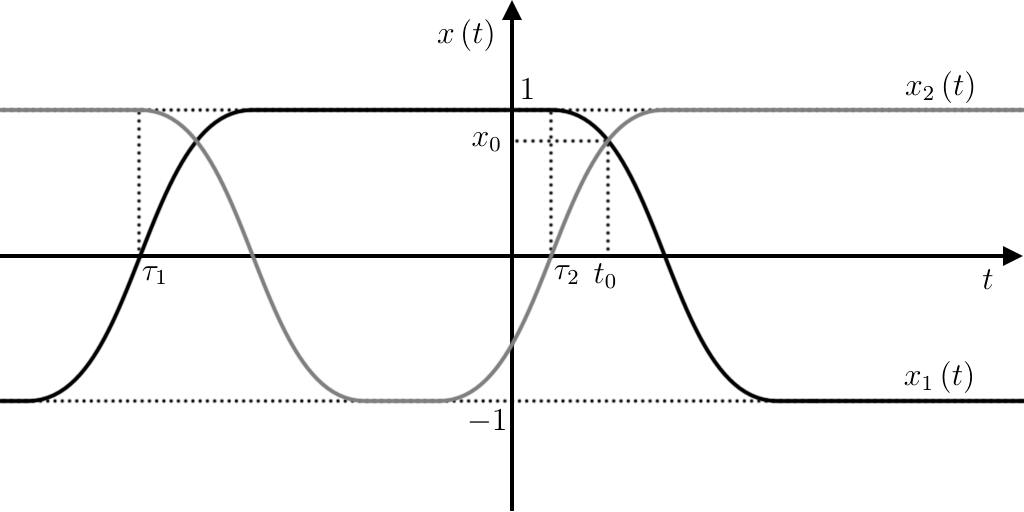
Mostrate che se \(-1{\lt}f(x){\lt}1\) per \(x∈ I\) intervallo aperto allora si ha che \(f\) è un arco di sinusoide per \(x∈ I\).
Mostrate che tutte le soluzioni sono \(C^ 1\), e che sono \(C^∞\) a tratti.
Vedrete che \(f≡ 1\) e \(f≡ -1\) sono inviluppi delle altre soluzioni, come spiegato nella sezione 22.4.
Soluzione nascosta: [UNACCESSIBLE UUID ’1QM’] [1QN] Sia \(f:[0,1]→ℝ\) una funzione \(C^ 2\) tale che \(f(0)=f(1)=0\) e \(f'(x)=f(x)f''(x)\) per ogni \(x∈[0,1]\).
Si provi che la funzione \(f\) è identicamente nulla.
Soluzione nascosta: [UNACCESSIBLE UUID ’1QP’][UNACCESSIBLE UUID ’1QQ’]