- E8
[0JN] An ear of a polygon is the triangle \(ABC\) formed by three consecutive vertices \(A,B,C\) of the polygon, such that the segment \(AC\) lies inside the polygon. This implies that the triangle \(ABC\) does not contain any point of the polygonal curve in its interior; and that the two segments \(AB,BC\) can be removed from the polygon and replaced with \(AC\) to create a newer polygon. Two ears are non-overlapping if their interiors do not intersect, or equivalently if the do not have a side in common.
Prove the Two ears theorem: every polygon with more than three vertices has at least two non-overlapping ears. (See [ 19 , 36 ] for more details).
(Hint: consider labelled polygons, to avoid the complication presented in figure 4.)
Solution 1
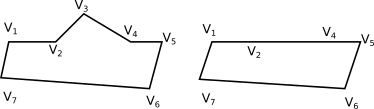
Figure 3 A polygon where, removing an ear, the number of unlabelled sides drops from 7 to 4.
EDB — 0JN
View
English
Authors:
"Mennucci , Andrea C. G."
.
Bibliography
Book index
- [21] G. H. Meisters. Polygons have ears. The American Mathematical Monthly, 82(6):648–651, 1975. ISSN 00029890, 19300972. DOI: 10.2307/2319703.
- [38] to3em. Two ears theorem — Wikipedia, the free encyclopedia, 2021. URL https://en.wikipedia.org/w/index.php?title=Two_ears_theorem&oldid=1024888322. [Online; accessed 13-novembre-2022].
Book index
- ear
- polygon, ear
- theorem, two ears —
Managing blob in: Multiple languages