: Polygons<a class="btn btn-sm" href="/UUID/EDB/2G3/?lang=eng"><span class="ttfamily"><small class="scriptsize">[2G3]</small></span></a>

9.1 Polygons[2G3]

We present some simple geometrical properties of polygons, that may be rigorously proven either by analytical methods (embedding geometrical objects as subsets of the Cartesian plane), or purely geometrical methods (in the spirit of [ 11 ] ).

In the following we will use the celebrated Jordan Theorem; a simple proof may be found in [ 26 ] .

Theorem 270

[2FW]Let $φ: [0,1] → ℝ^ 2$ be simple closed curve in the plane and $C=φ([0,1])$ be its trace. (See 418 for the definition). The complement $ℝ^ 2 ⧵ C$ consists of exactly two connected components, that are open. One of these components is bounded (and is called “the interior of the curve”, or, “the region bounded by the curve”) and the other is unbounded (the exterior). The curve $C$ is the boundary of each component.

The proof of the Jordan Theorem usually starts with a simple Lemma (again, see [ 26 ] ; or Theorem 6 [ 11 ] ).

Definition 271

[2G6]By polygonal curve $φ: [0,1] → ℝ^ 2$ we will mean: a not self-intersecting (that is, injective) polygonal (that is, piecewise linear) curve in the plane. Analytically, there are points $V_ 0,V_ 1,\ldots V_ n$ (called “vertices”) in the plane, and $0=t_ 0{\lt}t_ 1\ldots {\lt}t_ n=1$ such that

\[ φ (t) = \frac{t-t_ i}{t_{i+1}-t_ i} V_{i+1} + \frac{t_{i+1}-t}{t_{i+1}-t_ i} V_ i ~ \text{~ when~ }~ t_ i≤ t≤ t_{i+1}~ . \]

The polygonal curve is closed if $φ(0)=φ(1)$. (In this case we require that $φ$ is injective when restricted to $[0,1)$).

Lemma 272

[2FX]Let $C=𝜑([0,1])$, let $P$ be the region bounded by the closed polygonal curve, and $E$ the exterior; recall that $C,P,E$ is a partion of the plane. Choose $A,B∉ C$ and suppose that the segment $AB$ meets $C$ in $k$ points, none a vertex. Then: if $k$ is odd, $A,B$ are in different regions, $A∈ P⇔ B∉ P$; if $k$ is even, $A,B$ are in the same region, $A∈ P⇔ B∈ P$.

Definition 273

[2FN]A polygon is the plane figure bounded by the polygonal closed curve. ¹

Remark 274

[2CD]Consider a polygonal curve, with $n$ vertexes labeled $V_ 1,\ldots V_ n$; this bounds a polygon: how many sides does it have?

It depends. If some vertexes (in sequence) are aligned, then the figure in the plane will visually have less than $n$ sides and vertexes. For this reason, we will distinguish the unlabeled polygon (which is the subset of the plane) from the labeled polygon (in which we also take into account the position of the vertexes); the latter is less intuitive, but makes for better mathematics. See figure 2.

E274

[29Z]Difficulty:*.Let $n≥ 3$ integer; consider a polygon of $n+1$ vertices. Show that it can be cut in two polygons, one with $h$ and one with $k$ sides, and $3≤ h≤ n$, $3≤ k≤ n$. By "cut" we mean, two vertexes of the polygon (not contiguous) can be connected by a line that is internal and does not touch other vertexes or sides. The intersection of the two polygons is the segment $BD$, they do not have other points in common.

Hint. there is at least one vertex $B$ ”convex” in which the inner angle $𝛽$ is “convex” (i.e. $0{\lt}𝛽≤ 𝜋$ radians); call $A,C$ the vertexes contiguous to $B$; reason on the triangle $ABC$.

Hidden solution: [UNACCESSIBLE UUID ’1QT’]

E274

[1XH] Prove by induction that the sum of the internal angles of a polygon with $n≥ 3$ sides, is $(n-2)𝜋$.

(The proof is easy if the polygon is convex; in the general case 3 can be useful).

Hidden solution: [UNACCESSIBLE UUID ’1XM’]

E274

[0JN] An ear of a polygon is the triangle $ABC$ formed by three consecutive vertices $A,B,C$ of the polygon, such that the segment $AC$ lies inside the polygon. This implies that the triangle $ABC$ does not contain any point of the polygonal curve in its interior; and that the two segments $AB,BC$ can be removed from the polygon and replaced with $AC$ to create a newer polygon. Two ears are non-overlapping if their interiors do not intersect, or equivalently if the do not have a side in common.

Prove the Two ears theorem: every polygon with more than three vertices has at least two non-overlapping ears. (See [ 17 , 33 ] for more details).

(Hint: consider labelled polygons, to avoid the complication presented in figure 2.)

Hidden solution: [UNACCESSIBLE UUID ’2FV’]

$\includegraphics{UUID/2/F/T/blob_zxx.png}$

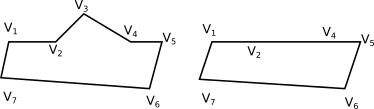
\includegraphics{UUID/2/F/R/blob_zxx.png} — Figure 2 A polygon where, removing an ear, the number of unlabelled sides drops from 7 to 4.

E274

[1XW] Difficulty:*. Show that each polygon can be “triangulated”, i.e. decomposed as a union of nonoverlapping triangles. ²

Hidden solution: [UNACCESSIBLE UUID ’1XX’]

E274

[2FP]Again, we say that a vertex $B$ is ”convex” if the inner angle $𝛽$ is “convex” (i.e. $0{\lt}𝛽≤ 𝜋$ radians). Prove that the polygon is convex if and only if all its vertices are convex. Hidden solution: [UNACCESSIBLE UUID ’2G5’]