: Poligoni<a class="btn btn-sm" href="/UUID/EDB/2G3/?lang=ita"><span class="ttfamily"><small class="scriptsize">[2G3]</small></span></a>

8.1 Poligoni[2G3]

Presentiamo alcune semplici proprietà geometriche dei poligoni, che possono essere rigorosamente provate sia con metodi analitici (incorporando oggetti geometrici come sottoinsiemi del piano cartesiano), o metodi puramente geometrici (nello spirito di [ 12 ] ).

Nel seguito useremo il celebre Teorema di Jordan; una semplice dimostrazione si può trovare in [ 27 ] .

Teorema 269

[2FW]Sia $φ: [0,1] → ℝ^ 2$ una curva semplice chiusa nel piano e $C=φ([0,1])$ sia il suo supporto. (Si veda 417 per la definizione). Il complementare $ℝ^ 2 ⧵ C$ è costituito esattamente da due componenti connesse, che sono aperte. Una di questi componenti è limitata (ed è chiamato ”l’interno della curva”, o anche ”la regione delimitata dalla curva”) e l’altro è illimitato (l’esterno). La curva $C$ è la frontiera di ognuna delle due componenti.

La dimostrazione del Teorema di Jordan inizia spesso con un semplice Lemma (di nuovo, si veda [ 27 ] ; o il Teorema 6 in [ 12 ] ).

Definizione 270

[2G6]Chiameremo “curva poligonale” una curva $φ: [0,1] → ℝ^ 2$ nel piano, spezzata (cioè, lineare a tratti) e non autointersecantesi (cioè, iniettiva). Analiticamente, vi sono punti $V_ 0,V_ 1,\ldots V_ n$ (chiamati “vertici”) nel piano, e vi sono $0=t_ 0{\lt}t_ 1\ldots {\lt}t_ n=1$ tali che

\[ φ (t) = \frac{t-t_ i}{t_{i+1}-t_ i} V_{i+1} + \frac{t_{i+1}-t}{t_{i+1}-t_ i} V_ i ~ \text{~ quando~ }~ t_ i≤ t≤ t_{i+1}~ . \]

La curva poligonale è chiusa se $φ(0)=φ(1)$. In questo caso richiediamo che $φ$ sia iniettiva quando ristretta a $[0,1)$.

Lemma 271

[2FX]Sia $C=𝜑([0,1])$, sia $P$ la regione delimitata dalla curva poligonale chiusa, e sia $E$ l’esterno; ricordiamo che $C,P,E$ è una partizione del piano. Fissiamo $A,B∉ C$ e supponiamo che il segmento $AB$ intersechi $C$ in $k$ punti, nessuno dei quali sia un vertice; allora, se $k$ è dispari $A,B$ sono in regioni diverse, cioè $A∈ P⇔ B∉ P$; se $k$ è pari, $A,B$ sono nella stessa regione.

Definizione 272

[2FN]Un poligono è la figura piana delimitata da una curva poligonale chiusa. ¹

Nota 273

[2CD]Consideriamo una curva poligonale, con $n$ vertici $V_ 1,\ldots V_ n$. Quanti lati ha il poligono che essa delimita?

Dipende. Se alcuni vertici in sequenza sono allineati, allora la figura nel piano avrà visivamente meno di $n$ lati e vertici. Per questo motivo, distingueremo il poligono non etichettato (che è il sottoinseme del piano) dal poligono etichettato (in cui teniamo conto anche della posizione dei vertici); il poligono etichettato è meno intuitivo, ma la trattazione matematica è più semplice. Si veda la figura 2.

E273

[29Z]Difficoltà:*.Sia $n≥ 3$ intero; consideriamo un poligono di $n+1$ vertici. Si mostri che può essere tagliato in due poligoni con rispettivamente $h,k$ lati, e $3≤ h≤ n$, $3≤ k≤ n$. Per "tagliare" intendiamo, collegare due vertici (non contigui) del poligono con un segmento che passa internamente, e che non tocca altri vertici o lati. L’intersezione dei due poligoni è il segmento $BD$, e non hanno altri punti in comune.

Sugg. esiste almeno un vertice $B$ in cui l’angolo interno $𝛽$ è “convesso” (cioè $0{\lt}𝛽≤ 𝜋$ radianti); siano $A,C$ i vertici contigui; si ragioni sul triangolo $ABC$.

Soluzione nascosta: [UNACCESSIBLE UUID ’1QT’]

E273

[1XH] Dimostrate per induzione che la somma degli angoli interni di un poligono di $n≥ 3$ lati è $(n-2)𝜋$.

(La dimostrazione è facile se il poligono è convesso; nel caso generale 3 può essere utile).

Soluzione nascosta: [UNACCESSIBLE UUID ’1XM’]

E273

[0JN] Un orecchio di un poligono è il triangolo $ABC$ formato da tre vertici consecutivi $A,B,C$ del poligono, tali che il segmento $AC$ si trova all’interno del poligono. Ciò implica che il triangolo $ABC$ non contiene alcun punto della curva poligonale al suo interno; e che i due segmenti $AB,BC$ possono essere rimossi dal poligono e sostituiti con $AC$ per creare un nuovo poligono. Due orecchie sono disgiunte se le loro parti interne non si intersecano, o in modo equivalente se non hanno un lato in comune.

Dimostrate il teorema delle due orecchie: ogni poligono (con almeno quattro vertici) ha almeno due orecchie disgiunte. (Vedere [ 18 , 42 ] per più dettagli).

(Sugg. considerate poligoni etichettati, per evitare le complicazioni di situazioni come quella presentata in figura 2.)

Soluzione nascosta: [UNACCESSIBLE UUID ’2FV’]

$\includegraphics{UUID/2/F/T/blob_zxx.png}$

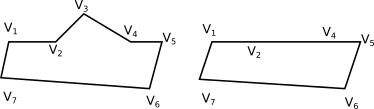
\includegraphics{UUID/2/F/R/blob_zxx.png} — Figura 2 Un poligono per cui la rimozione di un orecchio fa decrescere il numero di lati (non etichettati) da 7 a 4.

E273

[1XW] Difficoltà:*. Si mostri che ogni poligono può essere "triangolato", cioè decomposto come unione di triangoli che non si sovrappongono. ²

Soluzione nascosta: [UNACCESSIBLE UUID ’1XX’]

E273

[2FP]Di nuovo, diremo che un vertice $B$ è “convesso” se l’angolo interno $𝛽$ è convesso (cioè $0{\lt}𝛽≤ 𝜋$ radianti). Dimostrate che il poligono è convesso se e solo se tutti i suoi vertici sono convessi. Soluzione nascosta: [UNACCESSIBLE UUID ’2G5’]