23 Ordinary Differential equations[1QB]

To solve the following exercises, it is imporant to know some fundamental results, such as: the existence and uniqueness theorem ¹ , Gronwall’s Lemma; and in general some methods to analyze, solve and qualitative study Ordinary Differential Equations (abbreviated ODE). These may be found e.g. in [ 25 , 20 , 2 ] .

E418

[1QC]For each point $(x,y)$ of the plane with $x,y{\gt}0$ passes a single ellipses $4 x^ 2 + y^ 2 = a$ (with $a{\gt}0$). Describe the family of curves that at each point are orthogonal to the ellipse passing through that point. See figure 6.

Hidden solution: [UNACCESSIBLE UUID ’1QF’]

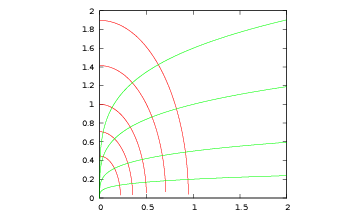
\includegraphics{UUID/1/Q/D/blob_zxx} — Figure 6 Ellipses (in red) and curves orthogonal to them.

[UNACCESSIBLE UUID ’1QG’]

[1QH] Prerequisites:3.

Let $I\subseteq {\mathbb {R}}$ be an open interval.

Let $F:I× ℝ→ (0,∞)$ be a positive continuous function, and let $f: I→ℝ$ be a differentiable function that solves the differential equation

\[ (f'(x))^ 2=F(x,f(x))\quad . \]

Prove that $x$ is, either always increasing, in which case $f'(x)=\sqrt{F(x,f(x))}$ for every $x$, or it is always decreasing, in which case $f'(x)=-\sqrt{F(x,f(x))}$; therefore $f$ is of class $C^ 1$.

Hidden solution: [UNACCESSIBLE UUID ’1QJ’] [1QK]Prerequisites:6.

Describe all the differentiable functions $f:ℝ→ℝ$ that solve

\[ ∀ x~ ,~ (f'(x))^ 2 + (f(x))^ 2 = 1~ . \]

Show that if $-1{\lt}f(x){\lt}1$ for $x∈ I$ open interval, then $f$ is a sine arc, for $x∈ I$.

Show that all solutions are $C^ 1$, and that they are piecewise $C^∞$.

Note that $f≡ 1$ and $f≡ -1$ are envelopes of the other solutions, as explained in the section 23.4.

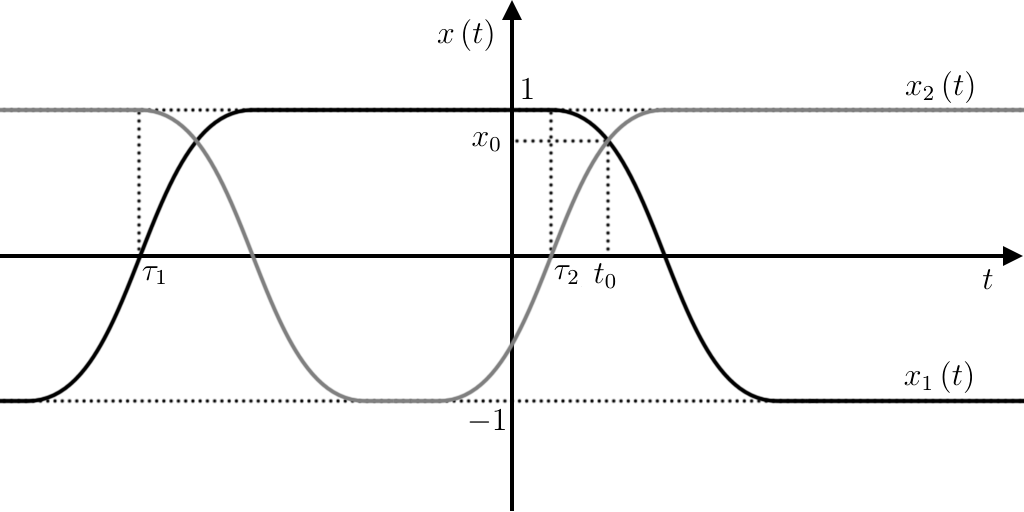
$\includegraphics{UUID/2/D/9/blob_zxx.png}$

Hidden solution: [UNACCESSIBLE UUID ’1QM’] [1QN] Let $f:[0,1]→ℝ$ be a function $C^ 2$ such that $f(0)=f(1)=0$ and $f'(x)=f(x)f''(x)$ for every $x∈[0,1]$.

Prove that the function $f$ is identically zero.

Hidden solution: [UNACCESSIBLE UUID ’1QP’][UNACCESSIBLE UUID ’1QQ’]