22.4 Envelope
Given a family of planar curves, we want to define the envelope curve. Let’s see two possible definitions.
Suppose the curves in the plane are described by the equation in implicit form \(F(x,y,a)=0\); that is, fixed the parameter \(a\), the curve is the locus
\[ \{ (x,y) : F(x,y,a)=0\} \quad ; \]Then the envelope is obtained by expliciting the variable \(a\) from the equation \(\frac{\partial ~ }{\partial {a}} F(x,y,a)=0\) and substituting it into the \(F(x,y,a)=0\).
For simplicity, consider curves that are functions of the abscissa. Let \(y=f(x,a)=f_ a(x)\) be a family of functions, with \(x∈ I,a∈ J\) (open intervals), then \(y=g(x)\) is the envelope of \(f_ a\) if the graph of \(g\) is covered by the union of the graphs of \(f_ a\) and the curve \(g\) is tangent to every \(f_ a\) where it touches it. More precisely, for every \(x∈ I\) there is \(a∈ J\) for which \(g(x)=f(x,a)\), and also, for every choice of \(a\) that satisfies \(g(x)=f(x,a)\), we have \(g'(x)=f'(x,a)\).
We want to see that the two previous definitions are equivalent in this sense.
- E438
[1RV]Let’s start with the first definition. Suppose we can apply the Implicit Function Theorem to the locus
\[ E_ a= \{ (x,a) : F(x,y,a)=0\} \quad ; \]Precisely, suppose that at a point \((\overline x,\overline y,\overline a)\) we have that \(\frac{\partial {}F}{\partial {y}} ≠ 0\). To this we also add the hypothesis \(\frac{\partial {}^ 2F}{\partial {aa}}≠ 0\). Fixed \(a\), you can express \(E_ a\) locally as a graph \(y=f(x,a)=f_ a(x)\). We also use the hypothesis \(\frac{\partial {}^ 2F}{\partial {aa}}≠ 0\) to express locally \(\frac{\partial {}F}{\partial {a}}= 0\) as a graph \(a=Φ(x,y)\). Defining \(G(x,y){\stackrel{.}{=}}F(x,y,Φ(x,y))\), show that \(G=0\) can be represented as \(y=g(x)\). Finally, show that \(g\) is the envelope of the curves \(f_ a\).
Hidden solution: [UNACCESSIBLE UUID ’1RW’][UNACCESSIBLE UUID ’1RX’]
- E438
[1RY]In the above hypotheses, assuming that \(\frac{\partial {}F}{\partial {y}} {\gt} 0\) and \(\frac{\partial {}^ 2F}{\partial {aa}}{\gt}0\), show that the envelope graph \(g\) is locally the ”edge” of the union of the graphs \(f_ a\) (in the sense that \(g(x)≥ f_ a(x)\) with equality for only one \(a\)).
Hidden solution: [UNACCESSIBLE UUID ’1RZ’][UNACCESSIBLE UUID ’1S0’]
- E438
[1S1]Note:From the text [ 19 ] , pg 84..Consider the curves
\[ y=f(x,a)=a x+\frac{a^ 2} 2 \]Find a differential equation solved by all curves. (Sugg. Eliminate \(a\) from the system \(y=f, y'=\frac{\partial ~ }{\partial {x}} f\). The result can be left in non-normal form.)
Calculate the envelope; check that it satisfies the differential equation obtained above.
See also the figure 10. Hidden solution: [UNACCESSIBLE UUID ’1S2’]
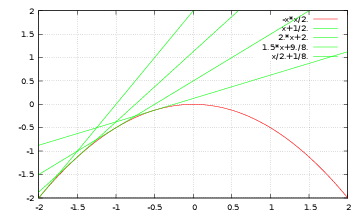
Figure 10 Solution of 3: envelope. - E438
[1S4]Consider ellipses \(a x^ 2 + y^ 2/a = 2\) (with \(a{\gt}0\)).
Find the region of the plane covered by these ellipses.
Show that the edge of this region is the envelope of ellipses, and describe it.
Hidden solution: [UNACCESSIBLE UUID ’1S5’][UNACCESSIBLE UUID ’1S6’]
- E438
[1S7]Let’s consider the lines \(a x + y/a = 1\) (with \(a{\gt}0\)).
Find the region of the first quadrant covered by these lines.
Show that the edge of this region is the envelope of the lines and describe it.
Hidden solution: [UNACCESSIBLE UUID ’1S8’]
- E438
[1S9]Let’s consider the straight lines
\[ \frac{x}{a} + \frac{y}{1-a} = 1 \]with \(x,y,a∈ (0,1)\). Describe the envelope curve.
Hidden solution: [UNACCESSIBLE UUID ’1SB’]