22.4 Inviluppo
Data una famiglia di curve planari, vogliamo definire la curva inviluppo. Vediamo due possibili definizioni.
Supponiamo che le curve nel piano siano descritte dall’equazione in forma implicita \(F(x,y,a)=0\); cioè, fissato il parametro \(a\), la curva è il luogo
\[ \{ (x,y) : F(x,y,a)=0\} \quad ; \]allora l’inviluppo si ottiene ricavando la \(a\) dalla equazione \(\frac{\partial ~ }{\partial {a}} F(x,y,a)=0\) e sostituendola nella \(F(x,y,a)=0\).
Per semplicità, consideriamo curve che sono funzioni dell’ascissa. Sia \(y=f(x,a)=f_ a(x)\) una famiglia di funzioni, con \(x∈ I,a∈ J\) (intervalli aperti), allora \(y=g(x)\) è l’inviluppo di \(f_ a\) se il grafico di \(g\) è coperto dall’unione dei grafici delle \(f_ a\) e la curva \(g\) è tangente a ogni \(f_ a\) laddove la tocca; più precisamente, per ogni \(x∈ I\) esiste \(a∈ J\) per cui \(g(x)=f(x,a)\), e inoltre, per ogni scelta di \(a\) che soddisfa \(g(x)=f(x,a)\), si ha \(g'(x)=f'(x,a)\).
Vogliamo vedere che le due precedenti definizioni sono equivalenti, in questo senso.
- E438
[1RV]Partiamo dalla prima definizione. Supponiamo di poter applicare il Teorema di Funzione Implicita al luogo
\[ E_ a= \{ (x,a) : F(x,y,a)=0\} \quad ; \]precisamente, supponiamo che in un punto \((\overline x,\overline y,\overline a)\) si abbia che \(\frac{\partial {}F}{\partial {y}} ≠ 0\). A questo aggiungiamo anche l’ipotesi \(\frac{\partial {}^ 2F}{\partial {aa}}≠ 0\). Fissato \(a\), si può esprimere \(E_ a\) localmente come grafico \(y=f(x,a)=f_ a(x)\). Usiamo inoltre l’ipotesi \(\frac{\partial {}^ 2F}{\partial {aa}}≠ 0\) per esprimere localmente \(\frac{\partial {}F}{\partial {a}}= 0\) come grafico \(a=Φ(x,y)\). Definito \(G(x,y){\stackrel{.}{=}}F(x,y,Φ(x,y))\), mostrate che \(G=0\) può essere rappresentato come \(y=g(x)\). Mostrate infine che \(g\) è l’inviluppo delle curve \(f_ a\).
Soluzione nascosta: [UNACCESSIBLE UUID ’1RW’][UNACCESSIBLE UUID ’1RX’]
- E438
[1RY]Nelle ipotesi precedenti, supponendo che \(\frac{\partial {}F}{\partial {y}} {\gt} 0\) e \(\frac{\partial {}^ 2F}{\partial {aa}}{\gt}0\), mostrate che il grafico dell’inviluppo \(g\) è localmente il “bordo” dell’unione dei grafici delle \(f_ a\), nel senso che \(g(x)≥ f_ a(x)\) con uguaglianza per un solo \(a\).
Soluzione nascosta: [UNACCESSIBLE UUID ’1RZ’][UNACCESSIBLE UUID ’1S0’]
- E438
[1S1]Note:Dal testo [ 20 ] , a pg 84..Consideriamo le curve
\[ y=f(x,a)=a x+\frac{a^ 2} 2 \]Trovate un equazione differenziale risolta da tutte le curve. (Sugg. Si elimini \(a\) dal sistema \(y=f, y'=\frac{\partial ~ }{\partial {x}} f\). Il risultato può essere lasciato in forma non normale.)
Calcolate l’inviluppo; verificate che soddisfa la equazione differenziale prima ottenuta.
Si veda anche la figura 10. Soluzione nascosta: [UNACCESSIBLE UUID ’1S2’]
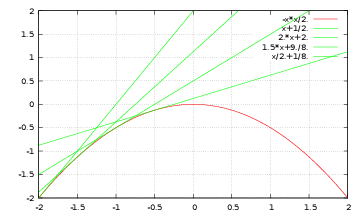
Figura 10 Soluzione di 3: inviluppo. - E438
[1S4]Consideriamo le ellissi \(a x^ 2 + y^ 2/a = 2\) (con \(a{\gt}0\)).
Trovate la regione del piano coperta da queste ellissi.
Mostrate che il bordo di questa regione è l’inviluppo delle ellissi, e descrivetelo.
Soluzione nascosta: [UNACCESSIBLE UUID ’1S5’][UNACCESSIBLE UUID ’1S6’]
- E438
[1S7]Consideriamo le rette \(a x + y/a = 1\) (con \(a{\gt}0\)).
Trovate la regione del primo quadrante coperta da queste rette.
Mostrate che il bordo di questa regione è l’inviluppo delle rette e descrivetelo.
Soluzione nascosta: [UNACCESSIBLE UUID ’1S8’]
- E438
[1S9]Consideriamo le rette
\[ \frac{x}{a} + \frac{y}{1-a} = 1 \]con \(x,y,a∈ (0,1)\). Descrivete la curva inviluppo.
Soluzione nascosta: [UNACCESSIBLE UUID ’1SB’]