- E3
-
Descrivete tutte le funzioni \(f:ℝ→ℝ\) differenziabili che risolvono
\[ ∀ x~ ,~ (f'(x))^ 2 + (f(x))^ 2 = 1~ . \]Mostrate che se \(-1{\lt}f(x){\lt}1\) per \(x∈ I\) intervallo aperto allora si ha che \(f\) è un arco di sinusoide per \(x∈ I\).
Mostrate che tutte le soluzioni sono \(C^ 1\), e che sono \(C^∞\) a tratti.
Vedrete che \(f≡ 1\) e \(f≡ -1\) sono inviluppi delle altre soluzioni, come spiegato nella sezione [1QB].
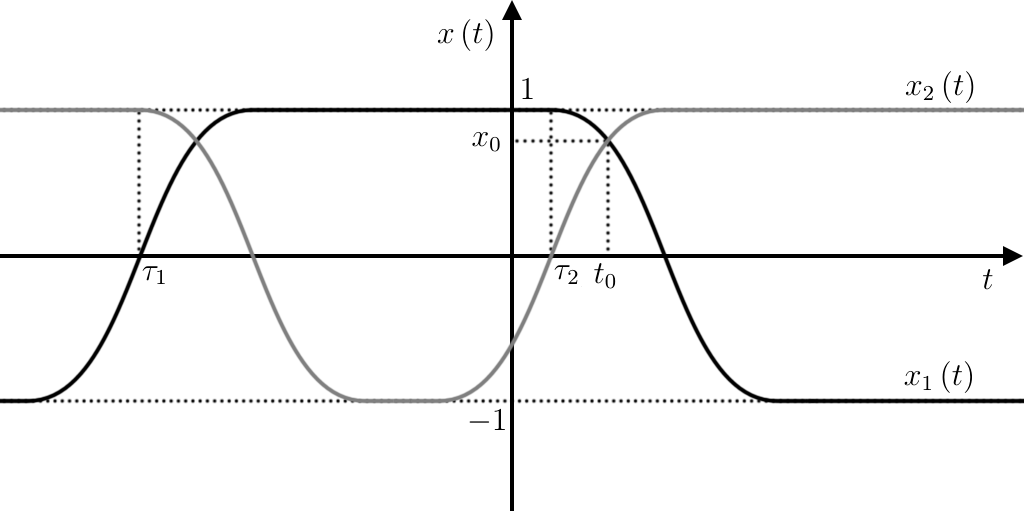 Soluzione 1
Soluzione 1
EDB — 1QK
Vista
Italiano
Autori:
"Mennucci , Andrea C. G."
.
Stai gestendo il blob in: Multiple languages